Info
These are the results from Modelling the NeoVAD using a GRNN
The average percentage error of the neural network initially decreased with the spread, until it reached a minimum at a value when the spread was 0.5, after which it started to increase.
Therefore, 0.5 was selected as the spread value for the neural network.
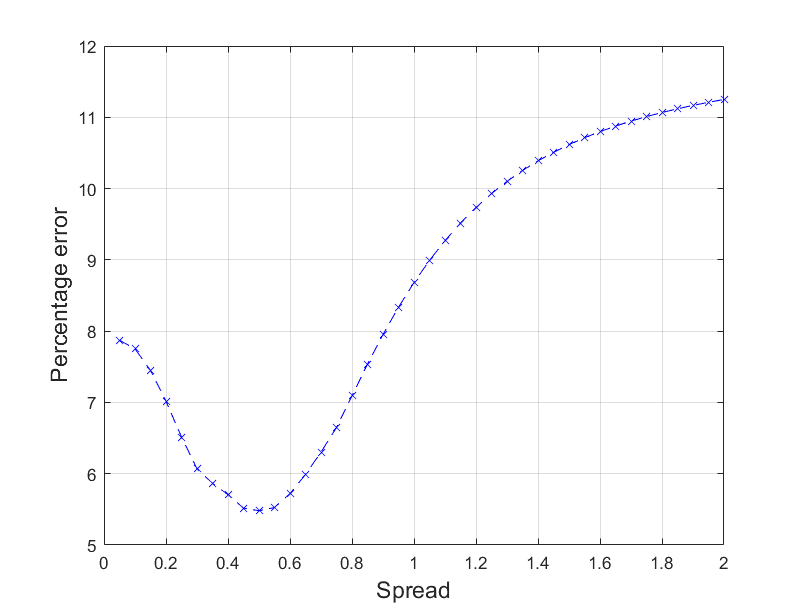 The variation of percentage error with the spread for the GRNN.
The variation of percentage error with the spread for the GRNN.
The neural network was created using the results from the experiments with an average error of 5.5%. This was a relatively low error margin given the limited dataset but may still be unacceptable for the project case.
The percentage error generally decreased as the number of experiments used to train the GRNN increased. The same training data was used as validation throughout this test for consistency. Providing more training data would likely result in a further decrease in average error.
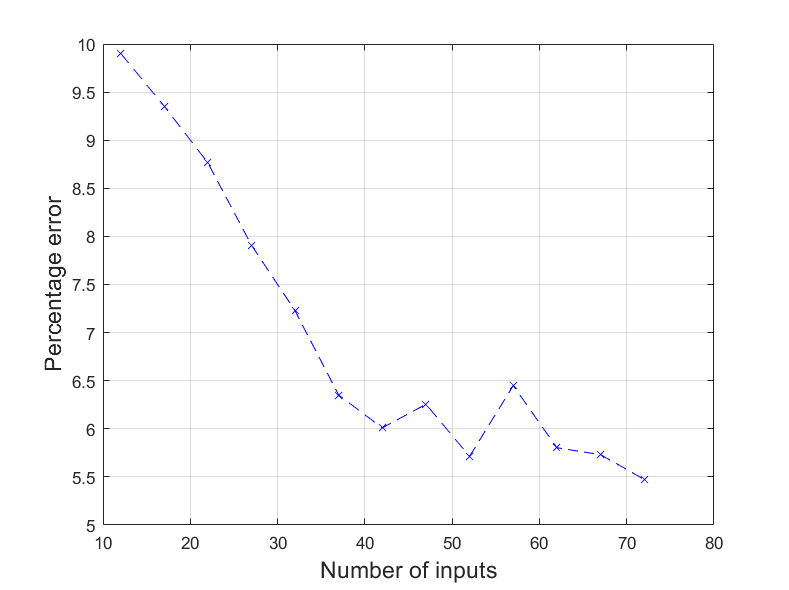 The variation of percentage error for the GRNN for increasing number of experiments used as training data.
The variation of percentage error for the GRNN for increasing number of experiments used as training data.
Another significant source of error may have been the range of results, which were between 26.3 and 78.3 mmHg. Mapping such a wide range of output values to five inputs with a limited dataset is likely to be inaccurate. This may be the reason why the error relationship was not a smooth fit, and there are portions of the plot where the error increases with the number of inputs; the error was heavily dependent on how close the training data was to the test data.
However, limiting the dataset to outputs between 53 and 68 mmHg (32 results in total) produced a GRNN with an average error of 8.3%, which was higher than the error with the full range and a similar amount of training data. This suggests that the range of the input values may have had a bigger impact on the accuracy. To investigate this further, the network could be tested with a limited input range. To mitigate this in future, the DoE could have been created with a more refined parameter range following a more thorough sensitivity analysis.
The method used to train the GRNN, and to determine the average error was relatively simple. The data was initially split such that the first 90% was used as training data, and the last 10% was used for testing. This method can lead to bias depending on what the last portion of the dataset contained, and the error can vary largely depending on which data points were used for validation. This was observed while training the GRNN, so a validation set that contained an appropriate spread of input parameters and output pressures was handpicked instead.
A more rigorous way to do this may be to implement a k-Fold Cross-Validation Method.